![]()
1. General non linear least squares non-linear function의 최솟값을 찾는 과정을 식으로 전개하면 위와 같다. 이때도 마찬가지로 loss에 해당하는 카이제곱을 구해야한다. 그러나 변수가 여러 개이므로 주어진 y식을 각 변수에 대해 편미분한 결과를 파악해두어야 한다. linear regression를 수행할 때와 마찬가지로 카이제곱 벡터가 0이 될때까지 기존의 값에서 카이제곱의 미분한 결과를 반복적으로 빼주어야 한다. 이때 dy / da_k는 y가 a1, a2로 구성된 식이므로 이를 계산하기 전 식을 나타내고 있다. 2. Fitting a non-linear function (Quiz) 비선형 함수를 적용할 수 있는 데이터 분포 고르기 카이제곱 식에 대해 올바른 설..
![]()
1. Simple linear regression 어떤 데이터들을 잘 설명하는 직선을 구할 수 있다. 데이터들을 기반으로 어떤 직선이 데이터의 분포를 가장 잘 표현할 수 있는지에 대해 고민하는 것이다. 이 직선으로 예측된 값이 실제값과 얼마나 떨어져있는지 확인하기 위한 식이 카이제곱이다. 실제값에서 예측값을 빼서 제곱한 값들을 모두 더한 것이 된다. 이 값이 곧 오차(loss)를 의미하게 되고 이를 최소화해야 우리가 원하는 최적의 직선을 얻을 수 있게 된다. 결국 이 오차를 끝까지 최소화하면 그 값은 0이 될 것이다. 따라서 카이제곱을 구성하는 변수인 m과 c에 대해 편미분을 수행하여 카이제곱벡터를 구하고, 이것이 영벡터와 같아지는 때가 언제인지 구하면 된다. 위 과정에서 c와 m에 대한 식을 정리할 수..
![]()
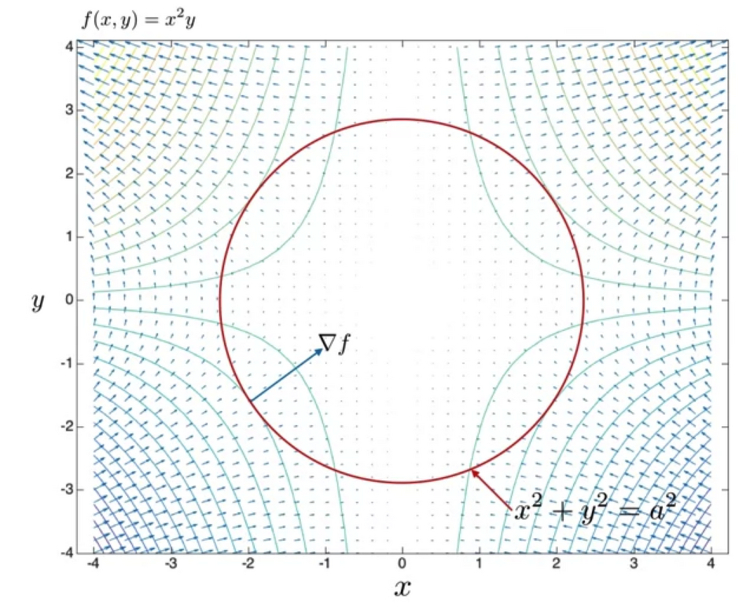
1. Constrained optimisation 이전에 다루었던 함수 f(x,y) = x^2y에 대해서 contour를 생성하면 오른쪽 그림과 같다. 우리는 gradient vector를 통해 최댓값을 갖는 x,y 지점에 이를 수 있다. 이때 최댓값에 이를 수 있는 x,y 쌍의 범위를 원의 형태로 제한(constraint)할 수 있고 이를 함수 g로 표현 가능하다. 위에서 살펴본대로 f의 값을 최대화하기 위해 제약(constraint) g 함수를 이용할 수 있다. 이때 두 벡터가 만나는 지점을 구하는 방정식에 Lagrange multiplier가 이용된다. 위 방정식을 통해 Lagrange multiplier를 구하고 이를 기존의 식에 다시 대입하여 x와 y의 식을 재구성한다. 결과적으로 f를 최대화,..
![]()
1. Welcome to Module 5! 최적의 평균과 분산을 구하는 방법에 대해 생각해보자. 어떤 함수에 대해 임의의 x값을 대입하고 그 미분계수를 통해 반복적으로 최적의 x값을 찾아나갈 수 있다. 이때 함수값을 미분계수로 나눈 값을 빼는 방식을 '반복(iterate)'하면 된다. 이런식으로 과정을 반복하는 방법을 'Newton-Raphson'이라고 부른다. 시작값을 잘못 설정하면 위와 같이 closed loop에 갇힐 수 있다. 혹은 너무 작은 미분계수를 갖는 점에서 시작하면 x의 변화량이 거의 없어서 의미 없는 학습을 반복하게될 가능성이 있다. 2. Newton-Raphson in one dimension (Quiz) 도함수 구하기 다항함수에 대해 미분을 수행한 결과를 직접 입력하면 된다. New..
![]()
1. Linearisation 기존 Taylor Series에서는 p로부터 얼마나 떨어져있는지를 기준으로 표현이 되었다. 이제 p를 델타 p 그리고 이것을 델타 x로 치환하여 표현한다. 실제 미분을 여러번 수행하면 그 결과값은 굉장히 작아지기 때문에 error로 보고 O로 묶어서 표현할 수 있게 된다. 심지어 f(x)에 대한 표현을 바꾸어 도함수를 기준으로 식을 정리하는 것도 가능하다. 2. Taylor series - Special cases (Quiz) odd function(기함수)은 원점대칭이고 even function(기함수)는 y축 대칭이다. 점근선이 존재하는 지점에서는 근사식을 구할 수 없다. 만약 그런 원함수에 대해 근사를 구하게 되면 approximation이 함수의 일부를 무시하거나 점..
![]()
1. Power series details 기존과 달리 Taylor series에서는 x=0이 아닌 어떤 point에서 접근해도 상관 없다고 본다. 따라서 여기서는 x = p로 가정하고 접근한다. Taylor Series에서 p = 0을 대입하면 기존의 Maclaurin Series와 동일해지는 것을 확인할 수 있다. 위에 정리된 식처럼 만약 2차식을 미분하게 되면 미분 과정에서 계수 때문에 2!이 분모가 될 것임을 짐작 가능하다. 이 과정을 일반화한 것이 Taylor Series가 된다. 2. Applyting the Taylor series (Quiz) 여러 f(x)에 대해 x = 0(Maclaurin) 또는 x = p(Taylor) 의 근사 함수를 구하는 문제가 출제된다. 이를 위해서 분수함수의 미..