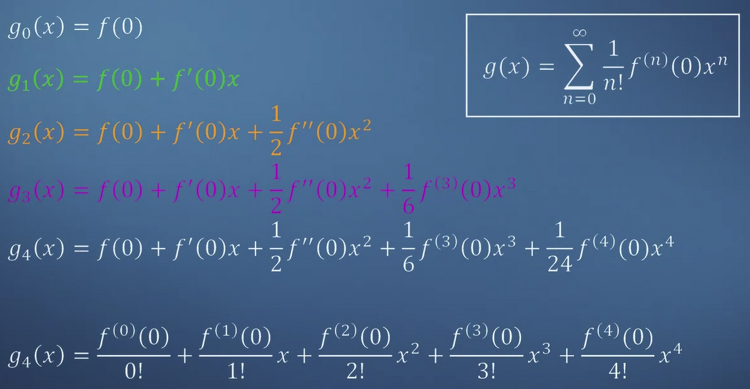Multivariate Calculus

1. Building approximations 1) 이 cooking book을 읽는 사람과 내가 비슷한 오븐을 쓴다고 가정 2) 치킨도 비슷하다고 가정 다른 조건들이 유사하다고 가정하면 변수들을 줄일 수 있고 이를 통해 간단한 식으로 근사할 수 있게 된다. 2. Power series Truncated series 주어진 함수 g의 변수를 하나씩 늘려나가면서 기존의 그래프와 얼마나 유사한지 확인하고 있다. 변수를 늘릴수록 기존의 그래프와 유사해지는 것을 볼 수 있다. 이런 방식으로 쭉 늘어놓은 함수의 모음을 truncated series라고 부른다. 3. Matching functions and approximations (Quiz) 기존의 그래프를 보고 적절한 근사를 고르는 문제들이 출제되어 있다...

1. Simple neural networks neural network를 이루는 작은 원 하나를 neuron이라고 한다. 그 구조는 활성화 함수인 시그모이드에 가중치 w와 입력 a를 곱하고 b를 더한 값을 집어넣는 것이다. 만약 입력이 여러개이고 이것이 여러개로 구성된 다음층으로 전달될 때는 위와 같은 구조를 가진다. 1번 layer에 속하는 neuron들이 0번 layer에 속하는 neuron들과 모두 연결되어있다. 그리고 그 연결은 위에서 설명한 가중치와의 곱 + 편향으로 구성된다. 이를 일반화하면 단순한 숫자(scalar)의 곱이 아닌 벡터의 곱으로 이해할 수 있게 된다. 가중치벡터 W와 입력벡터 a를 곱하고 여기에 편향벡터 b를 더한 결과를 시그모이드 함수에 집어넣는 것이다. 다양한 일들을 수행..

1. Multivariate chain rule t에 관한 n개의 함수 x로 구성된 함수 f를 t에 대해 미분하는 것은 chain rule로 표현 가능하다. 이때 편미분벡터와 미분벡터를 내적하는 꼴이 된다. 2. More multivariate chain rule 앞서 배운 내용처럼 chain rule은 원래 단변수함수를 바로 미분한 것과 동일한 결과를 가진다. 하지만 벡터를 원소로 가지는 경우 위처럼 행렬의 편미분과 미분의 곱으로 표현된다. 위 예시에서 앞의 두 개는 Jacobian(편미분을 모아놓은 벡터)이고 행렬의 곱에 따라 1 x 1 사이즈의 결과가 나타난다. 따라서 계산결과는 scalar값이 된다. 3. Multivariate chain rule exercise multivariate chain..

1. The Sandpit 간단한 함수에 대해서는 값이 최대가 되는 좌표가 어디인지 파악하기가 쉽다. 위 그래프는 Jacobian vector를 통해 표현한 것이다. 그러나 대부분은 이렇게 간단하지는 않다. 앞서 다루었던 복잡한 식을 표현하면 위와 같다. 여기서는 global maximum A와 local maximum C,E가 존재한다. 반대로 global minimum D와 local minimum B가 존재한다. 얼마나 가파른지에 대한(gradient) 정보를 각 좌표를 기준으로 표시하면 아래 그래프와 같다. 우리는 모든 것을 관망하는 입장에서 어디로 가야 가장 높은지 혹은 가장 낮은지를 알 수 있다. 하지만 실제로는 모든 데이터에 대한 정보를 파악하고 미리 알 수는 없으므로 마치 밤길을 거니는 것..

1. The Jacobian J is a vector pointing the direction of steepest slope of this function. J는 여러 개의 변수로 구성된 함수 f의 각 변수에 대해 편미분한 것들을 모아놓은 벡터이다. x,y축에 따른 z의 값이 표현된 좌표평면이다. z의 값이 클수록 밝게 표시되고, z의 값이 작을수록 어둡게 표시된다. 이를 등고선으로 표현하면 위와 같다. 여기서 어떤 것의 J 값이 가장 클까? z의 값이 가장 크다고 표현된 A의 J 값이 가장 크고, 가장 어두운 곳에 위치한 B의 J 값이 가장 작은 것이다. 2. Calculating the Jacobian Jacobian(편미분 벡터)를 구하기(3문제) Jacobian에 특정 값 대입하여 계산하기(2문..

1. Variables, constants & context time은 독립변수, speed는 종속변수다. 즉, speed가 time이 커짐에 따라 변화하는 것이지 그 반대가 아니라는 뜻이다. 우리는 이처럼 그래프가 지니는 의미를 파악하고 미분을 결정해야한다. 우리가 수행하는 미분은 '종속변수'에 대한 것이다. 이 예시에서 F는 a와 v에 의해 결정되는 종속변수라고 생각된다. 그리고 m과 d는 상수이다. 하지만 speed에 대한 식에 F가 영향을 주는 경우에서 F는 독립변수가 된다. 또 자동차를 제작하는 상황이라고 한다면 m,d도 독립변수가 될 수 있을 것이다. m에 관한 식에는 h,r,t,p(roh)라는 네 개의 변수가 존재한다. 따라서 1D에 대한 미분을 그대로 수행할 수 없다. 여러 개의 변수가 존..